69. x 的平方根(Sqrt(x))E
英文题目
Given a non-negative integer x, compute and return the square root of x.
Since the return type is an integer, the decimal digits are truncated, and only the integer part of the result is returned.
Example 1:
Input: x = 4 Output: 2Example 2:
Input: x = 8 Output: 2 Explanation: The square root of 8 is 2.82842..., and since the decimal part is truncated, 2 is returned.Constraints:
0 <= x <= 2^{31} - 1
中文题目
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
输入: 4 输出: 2示例 2:
输入: 8 输出: 2 说明: 8 的平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
调用库函数
时间复杂度O(1),空间复杂度O(1)
# python3: 时间 44 ms, 击败 77.67%; 内存 16 MB, 击败 48.32% class Solution: def mySqrt(self, x: int) -> int: return int(x ** 0.5)// c++: 时间 8 ms, 击败 19.27%; 内存 6 MB, 击败 5.10% // sqrt来源于头文件cmath class Solution { public: int mySqrt(int x) { return sqrt(x); } };// java: 时间 1 ms, 击败 93.71%; 内存 38.6 MB, 击败 56.11% class Solution { public int mySqrt(int x) { // 注意转换 return (int)Math.sqrt(x); } }// go: 时间 0 ms, 击败 100%; 内存 2 MB, 击败 16.59% func mySqrt(x int) int { return int(math.Sqrt(float64(x))) }// javascript: 时间 56 ms, 击败 98.69%; 内存 41.5 MB, 击败 91.26% /** * @param {number} x * @return {number} */ var mySqrt = function(x) { return Math.floor(Math.sqrt(x)); };
袖珍计算器算法
借助指数函数exp和对数函数ln代替平方根函数
由于计算机无法存储浮点数的精确值,而指数函数和对数函数的参数和返回值均为浮点数,因此运算过程中会存在误差
例如当 x = 2147395600 时, 的计算结果与正确值 46340 相差 ,这样在对结果取整数部分时,会得到 46339 这个错误的结果
因此在得到结果的整数部分 ans 后,应判断 ans+1 的平方是否小于等于 x,如果是,则 ans+1 为真正的答案
时间复杂度O(1),空间复杂度O(1)
# python3: 时间 36 ms, 击败 95.78%; 内存 15.9 MB, 击败 60.57% class Solution: def mySqrt(self, x: int) -> int: if x == 0: return 0 res = int(math.exp(0.5 * math.log(x))) return (res + 1) if (res+1)**2 <= x else res// c++: 时间 0 ms, 击败 100%; 内存 6.1 MB, 击败 5.10% class Solution { public: int mySqrt(int x) { if (x == 0) { return x; } int res = exp(0.5 * log(x)); return ((long long)(res+1)*(res+1) <= x) ? res + 1 : res; } };// java: 时间 0 ms, 击败 100%; 内存 38.7 MB, 击败 43.74% class Solution { public int mySqrt(int x) { if (x == 0) { return x; } int res = (int)Math.exp(0.5 * Math.log(x)); return (long)(res+1)*(res+1) <= x ? res + 1 : res; } }// go: 时间 0 ms, 击败 100%; 内存 2 MB, 击败 16.59% func mySqrt(x int) int { if x == 0 { return 0 } res := int(math.Exp(0.5 * math.Log(float64(x)))) if (res + 1) * (res + 1) <= x { return res + 1 } return res }// javascript: 时间 60 ms, 击败 97.4%; 内存 42.3 MB, 击败 61.75% /** * @param {number} x * @return {number} */ var mySqrt = function(x) { if (x == 0) { return x; } let res = Math.floor(Math.exp(0.5 * Math.log(x))); return (res+1)*(res+1) <= x ? res + 1 : res; };
二分查找法
由于x平方根的整数部分 ans 是满足 的最大 ans 值,因此可对 ans 进行找两端为闭区间的右侧边界的二分查找, 其中下界为0,上界为 x
时间复杂度O(log x),空间复杂度O(1)
# python3: 时间 44 ms, 击败 77.67%; 内存 15.9 MB, 击败 59.22% class Solution: def mySqrt(self, x: int) -> int: l, r = 0, x while l <= r: mid = l + (r - l) // 2 if mid ** 2 <= x: l = mid + 1 else: r = mid - 1 return l - 1// c++: 时间 0 ms, 击败 100%; 内存 5.8 MB, 击败 39.22% class Solution { public: int mySqrt(int x) { int l = 0, r = x; while (l <= r) { int mid = l + (r - l) / 2; if ((long long)mid * mid <= x) { l = mid + 1; } else { r = mid - 1; } } return l - 1; } };// java: 时间 1 ms, 击败 93.71%; 内存 38.5 MB, 击败 78.7% class Solution { public int mySqrt(int x) { int l = 0, r = x; while (l <= r) { int mid = l + (r - l) / 2; if ((long)mid * mid <= x) { l = mid + 1; } else { r = mid - 1; } } return l - 1; } }// go: 时间 4 ms, 击败 41.70%; 内存 2 MB, 击败 16.59% func mySqrt(x int) int { l, r := 0, x for l <= r { mid := l + (r - l) / 2 if mid * mid <= x { l = mid + 1 } else { r = mid - 1 } } return l - 1 }// javascript: 时间 76 ms, 击败 59.17%; 内存 42.3 MB, 击败 62.92% /** * @param {number} x * @return {number} */ var mySqrt = function(x) { let l = 0, r = x; while (l <= r) { let mid = l + Math.floor((r - l) / 2); if (mid * mid <= x) { l = mid + 1; } else { r = mid - 1; } } return l - 1; };
梯度下降法
参考:https://blog.csdn.net/dpengwang/article/details/99092278
主要是通过求梯度为0的点,得到凸函数的全局最小值
首先构建损失函数为凸函数的目标函数,使得目标函数的最小值对应的是要求的值
设 t 为待求的 target,此处即为题目 x,而公式中的 x 是迭代过程的未知数,做一下转化更易懂
由构建的损失函数为
求损失函数的梯度
得到迭代公式为,其中a为学习率
然后给x一个初始值,然后不断通过迭代公式更新x,即可逼近最小值
# 这只能通过约t <= 8000以下,更大的数字不能收敛 class Solution: # 请注意,此处的参数原题是 x, # 为了更好理解改为了 t, 而 x 用于迭代过程,和公式相匹配 def mySqrt(self, t: int) -> int: # 初始值,注意,初始值不能设为0,否则所有迭代结果均为0 x = 1 # 定义学习率 learning_rate = 0.00001 # 定义精度 eps = 0.01 while math.fabs(x ** 2 - t) > eps: # 梯度下降迭代过程 x = x - learning_rate * self.gradient(x, t) res = int(x) # 注意边界值,因为 int 会向下取整,所以需判断 int+1 是否更接近答案 return (res + 1) if (res+1)**2 <= t else res def gradient(self, x, t): return 4 * x * (x ** 2 - t)
牛顿迭代法
牛顿迭代法是一种可快速求解函数零点的方法
可用C表示待求出平方根的那个整数。显然,C的平方根就是函数的零点
牛顿迭代法的本质是借助泰勒级数,从初始值开始快速向零点逼近。
任取一个作为初始值,在每一步的迭代中,找到函数图像上的点,过该点作一条斜率为该点导数的直线,与横轴的交点记为。相对而言距离零点更近。在经过多次迭代后,就可得到一个距离零点非常接近的交点
下图是从开始迭代两次,得到和的过程
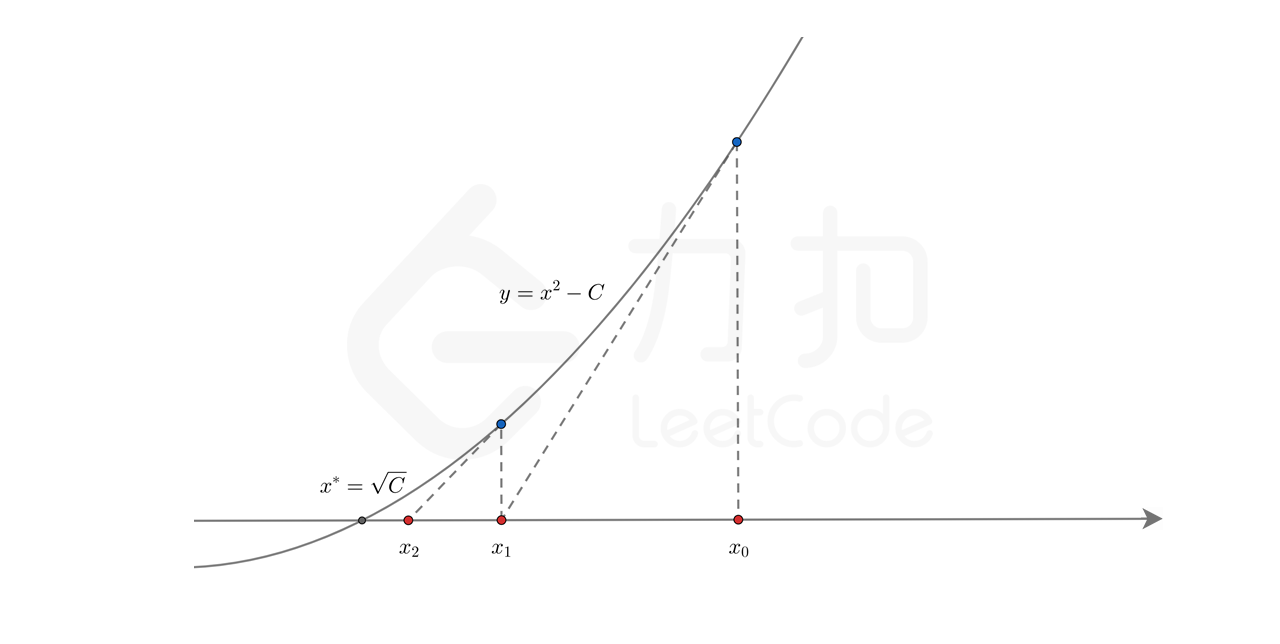
1.首先选择作为初始值
2.在每一步迭代中,通过当前的交点,找到函数图像上的点,作一条斜率为的直线,直线的方程为
3.与横轴的交点的方差的解,即为新的迭代结果
在进行k次迭代后,的值与真实的零点足够接近,即可作为答案
# python3: 时间 44 ms, 击败 79.23%; 内存 14.7 MB, 击败 85.31% class Solution: def mySqrt(self, x: int) -> int: if x == 0: return 0 C, x0 = float(x), float(x) while True: xi = 0.5 * (x0 + C / x0) if abs(x0 - xi) < 1e-7: break x0 = xi return int(x0)
